Defining Sound: How it Occurs and What Induces It

It’s a bustling afternoon, and just like any normal day, you notice the world around you is alive with unseen forces. One moment, your phone buzzes with an incoming message, resting silently on the table, yet creating a distinct tremor. Not just that, as you listen to your favorite song, the bass vibrates through your chest, a tangible presence from an invisible source. Careless as you might be, taking it as a trivial matter, your body isn’t joking about it. In that instant, your ears and skin were tuned into a symphony of pressure and rarefaction, a delicate ballet of particles that carried information and energy. This is what we call “sound.

Sound, those subtle whispers and powerful roars, may seem magical, but it’s just physics. In simple terms, sound is the vibration that travels through a medium as an audible wave. Normally, when an object vibrates, it pushes and pulls on the surrounding particles (like air molecules), creating areas of high pressure (compressions) and low pressure (rarefactions). These compressions and rarefactions then travel outward from the source, transferring energy without transferring matter. In fact, ancient Greek philosophers like Pythagoras first observed this phenomenon; they noticed that the length of a vibrating string directly influenced the pitch of the sound it produced. Seeing this harmonious effect, the study of acoustics was eventually given its name based on the Greek word akouein, meaning “to hear.”

The medium plays an important role in this microscopic effect. Sound needs something to travel through, whether it’s air, water, or even solid ground. Imagine a chain of people: if the first person pushes the next, that push travels down the line. Similarly, in a gas like air, molecules bump into each other, passing the vibration along. This is why you can’t hear anything in the vacuum of space; there are no particles to transmit the vibrations. Water, being denser than air, allows sound to travel much faster, which is why whales can communicate across vast oceanic distances. Solids, with their tightly packed molecules, are even better conductors of sound, which is why a knock on one end of a table can be heard clearly at the other.

Temperature also influences the speed of sound. Heat makes atoms and molecules move more rapidly and randomly. This increased motion means that vibrations can be passed along more quickly. Cold conditions slow down molecular motion, which in turn slows the propagation of sound, which is why sounds might seem to travel differently on a crisp winter morning compared to a warm summer day.

How Sound Affects Our Daily Lives

The effects of sound are all around us: the gentle rustle of leaves, the intricate melodies of a symphony, the urgent blare of a car horn, the deep rumble of an earthquake. These everyday events convey the same physics as the sophisticated technology in a concert hall. And this is not an exaggeration. In a rock concert, the sheer energy of the sound waves is strong enough to physically move air, making you feel the music as much as hear it. Even the softest whisper happens when tiny pressure waves created by your vocal cords propagate through the air to another person’s ear.

Speaking of sound, these wave-like phenomena are just an application of vibrations on a massive scale. Inside a guitar, a vibrating string causes the air inside the guitar’s body to vibrate, amplifying the sound. The difference is that, compared to a single vibrating string, a full orchestra involves hundreds of instruments, each producing complex vibrations that interact to create a rich tapestry of sound. The vibrations from different instruments superimpose on each other, creating constructive (louder) and destructive (quieter) interference, shaping the overall soundscape. When these vibrations are strong enough to overcome the insulating properties of the air, they reach our eardrums, causing them to vibrate in turn, producing the brilliant channels of information we call hearing.

The amount of energy involved in sound can vary dramatically. A typical whisper might carry only a few picowatts of power, barely enough to register. To put this in perspective with other forms of sound, if you could somehow collect all the sound energy from every library in a major city for an entire day, you still wouldn’t approach the power involved in a single jet engine taking off. Even on a small scale, engineers still exploit sound: medical ultrasound literally uses high-frequency sound waves to image internal organs without invasive surgery. Furthermore, sonar systems use sound waves to map the ocean floor and detect underwater objects. Even some industrial processes rely on sound to clean delicate parts or to detect flaws in materials using non-destructive testing.

How Many Decibels Can Cause Damage? (Quantitative Analysis)

Imagine that, on another day, you’re attending a rock concert. As the band launches into their set, you suddenly feel the floor vibrating with the sheer force of the sound. We’ve already talked about how loud music, made of just a few watts, isn’t harmful at all. But the idea of getting hurt one day sticks with you, and you ask:

“What if it wasn’t just a few watts? How much intensity would it actually take for this to stop being an exhilarating experience and start becoming something… dangerous?”

We’ll define “dangerous” as prolonged exposure to 120 decibels (dB), which is roughly the threshold of pain and can cause immediate hearing damage over short periods. The decibel scale is logarithmic, meaning a small increase in dB represents a large increase in sound intensity.

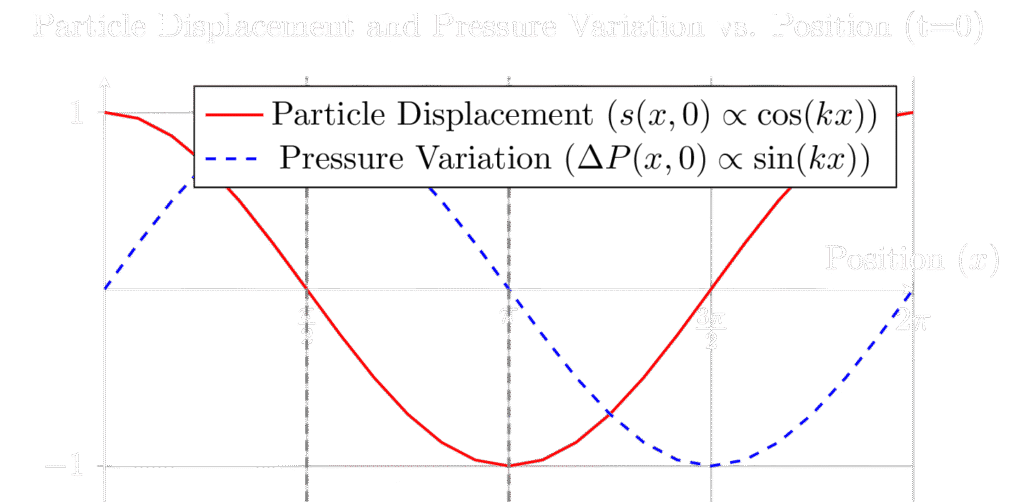
To break down this problem, we first need to understand how sound propagates. A simple sound wave can be described as a longitudinal wave, where particles oscillate back and forth in the same direction as the wave’s travel. The displacement of a particle from its equilibrium position, s(x, t), can be modeled by a sinusoidal function:

s(x, t) = s_{max} \cos(kx - \omega t)

where s_max is the maximum displacement, k is the wave number (k = 2π/λ), Ω is the angular frequency (Ω = 2πf), x is the position, and t is time.

The pressure variation, ΔP(x, t), in a sound wave is proportional to the rate of change of displacement with respect to position. This is where calculus comes in:

\Delta P(x, t) = -\rho v^2 \frac{\partial s}{\partial x}

Taking the partial derivative of s(x, t) with respect to x:

\begin{align*}
\frac{\partial s}{\partial x} &= \frac{\partial}{\partial x} [s_{max} \cos(kx - \omega t)]\\ &= -s_{max} k \sin(kx - \omega t)
\end{align*}

Substituting this back into the pressure variation equation:

\begin{align*}
    \Delta P(x, t) &= -\rho v^2 [-s_{max} k \sin(kx - \omega t)] \\&= (\rho v^2 s_{max} k) \sin(kx - \omega t)
\end{align*}

The maximum pressure variation, ΔP_max, is thus:

\Delta P_{max} = \rho v^2 s_{max} k

The intensity (I) of a sound wave, which is the average power per unit area, is directly related to the maximum pressure variation:

I = \frac{(\Delta P_{max})^2}{2\rho v}

where ρ is the density of the medium (for air, ρ ≈ 1.225 kg/m³) and v is the speed of sound in the medium (for air at room temperature, v ≈ 343 m/s).

First, let’s determine the sound intensity (I) corresponding to 120 dB. The sound intensity level (β) in decibels is given by:

\beta = 10 \log_{10}\left(\frac{I}{I_0}\right)

where I₀ is the reference intensity, the threshold of human hearing, I₀ = 10^-12 W/m².

120 \text{ dB} = 10 \log_{10}\left(\frac{I}{10^{-12} \text{ W/m}^2}\right)

12 = \log_{10}\left(\frac{I}{10^{-12} \text{ W/m}^2}\right)

10^{12} = \frac{I}{10^{-12} \text{ W/m}^2}

I = 10^{12} \times 10^{-12} \text{ W/m}^2 = 1 \text{ W/m}^2

This is 1 Watt per square meter, an intensity large enough to cause real pain and potential permanent hearing loss after sustained exposure.

Now, we can use this intensity to find the maximum pressure variation, ΔP_max:

\begin{align*}
    \Delta P_{max} &= \sqrt{2 \rho v I}\\
     &= \sqrt{2 \times 1.22 \text{ kg/m}^3 \times 343 \text{ m/s} \times 1 \text{ W/m}^2}\\
     &=\approx \sqrt{840.05} \text{ Pa} \approx 28.98 \text{ Pa}
\end{align*}

This is approximately 29 Pascals of pressure fluctuation. To put that in perspective, the standard atmospheric pressure is around 101,325 Pascals. So, while 29 Pa might seem small, it’s a significant and rapid pressure change that your eardrum experiences.

Finally, we can even calculate the maximum particle displacement, s_max, if we assume a typical frequency, say f = 1000 Hz (a common test frequency for hearing). First, find the angular frequency Ω = 2πf = 2π(1000 Hz) = 2000π rad/s.

Then, the wave number k = Ω/v = (2000π rad/s) / (343 m/s) ≈ 18.3 m^-1.

From P_max = ρv²s_maxk, we can solve for s_max:

\begin{align*}
s_{max} &= \frac{\Delta P_{max}}{\rho v^2 k}\\
&=\frac{28.98 \text{ Pa}}{1.225 \text{ kg/m}^3 \times (343 \text{ m/s})^2 \times 18.3 \text{ m}^{-1}}\\
&\approx 1.1 \times 10^{-5} \text{ m}
\end{align*}

This means the air particles are oscillating back and forth by only about 11 micrometers roughly the size of a red blood cell to produce a sound loud enough to cause pain! This tiny, rapid movement is a testament to the efficient transfer of sound energy.

Realistically, to experience 120 dB, you’d have to be very close to a powerful sound source, like a jet engine at takeoff (around 30 meters away) or a very loud rock concert speaker. Fortunately, most everyday sounds are far below this threshold, and your ears have mechanisms to protect themselves, though prolonged exposure can still cause damage.

Computational Analysis: Simulating the Sound Wave

Beyond theoretical calculations, modern physics relies heavily on computational modeling to understand and predict complex phenomena. For sound, we can use programming to directly generate and visualize the wave’s behavior based on the mathematical functions derived from calculus. This allows us to “see” the intricate mechanics of particles and pressure that constitute sound.

Let’s use Python to compute the particle displacement s(x, t) and pressure variation ΔP(x, t) for a sound wave across a spatial range at a specific moment in time. This is like taking a snapshot of the wave as it travels.

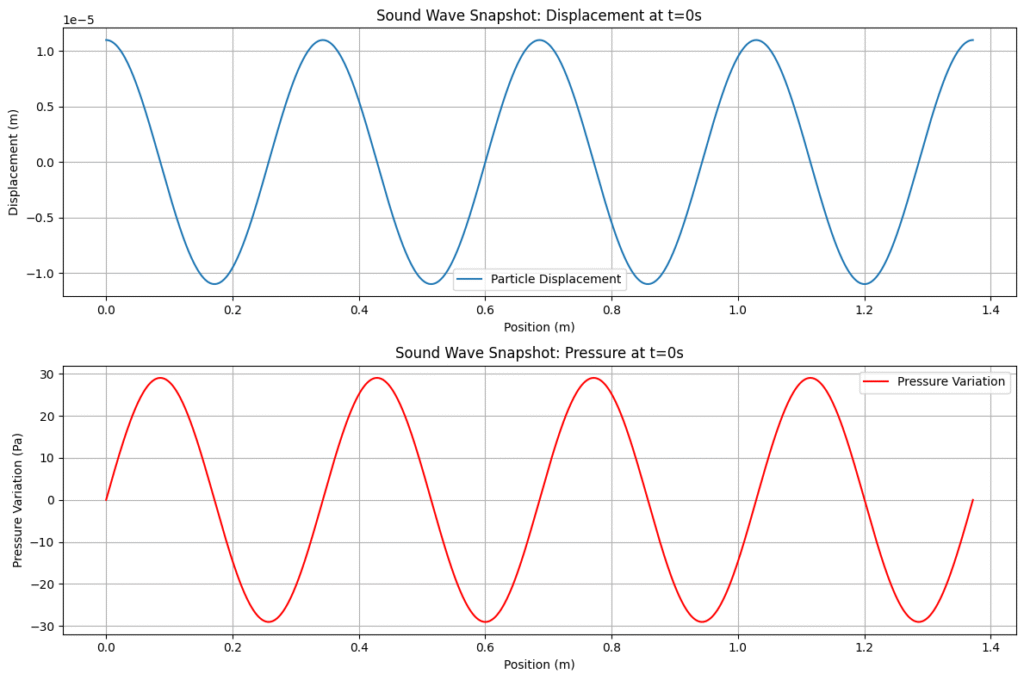
The Python code detailed here, simulates a snapshot of a sound wave based on the mathematical relationships we’ve discussed, you can run it yourself and see how it works.

import numpy as np
import matplotlib.pyplot as plt


# --- Physical Constants for Air at Room Temperature ---
rho = 1.225  # kg/m^3 (density of air)
v = 343      # m/s   (speed of sound in air)

# --- Wave Parameters (example values from previous calculation) ---
s_max = 1.1e-5     # meters (maximum particle displacement)
frequency = 1000   # Hz (frequency of the wave)
omega = 2 * np.pi * frequency # Angular frequency (rad/s)
k = omega / v                 # Wave number (rad/m)

# Calculate maximum pressure variation based on derived relation
delta_P_max = rho * v**2 * s_max * k

print(f"Sound Wave Simulation")
print(f"Max Displacement (s_max): {s_max:.2e} m")
print(f"Frequency: {frequency} Hz")
print(f"Calculated Max Pressure Variation (Delta P_max): {delta_P_max:.2f} Pa\n")

# --- Spatial Domain for Snapshot ---
# We'll observe the wave over a range of positions (e.g., 4 wavelengths)
wavelength = v / frequency
x_values = np.linspace(0, 4 * wavelength, 1000) # 1000 points over 4 wavelengths

# --- Time Snapshot ---
t_snapshot = 0  # seconds (let's look at the wave at time t=0)

# --- Calculate Displacement and Pressure at t_snapshot for each x ---
# Using the derived sinusoidal functions:
s_values = s_max * np.cos(k * x_values - omega * t_snapshot)
delta_P_values = delta_P_max * np.sin(k * x_values - omega * t_snapshot)

# ---Plotting Results ---
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(x_values, s_values, label='Particle Displacement')
plt.title(f'Sound Wave Snapshot: Displacement at t={t_snapshot}s')
plt.xlabel('Position (m)')
plt.ylabel('Displacement (m)')
plt.grid(True)
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(x_values, delta_P_values, color='red', label='Pressure Variation')
plt.title(f'Sound Wave Snapshot: Pressure at t={t_snapshot}s')
plt.xlabel('Position (m)')
plt.ylabel('Pressure Variation (Pa)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

This computational approach allows us to numerically explore the wave equations, visualizing the intricate, synchronized mechanics of particles and pressure that our ears interpret as sound. The output of this Python code, displayed below, clearly shows the two sinusoidal waves for particle displacement and pressure variation.

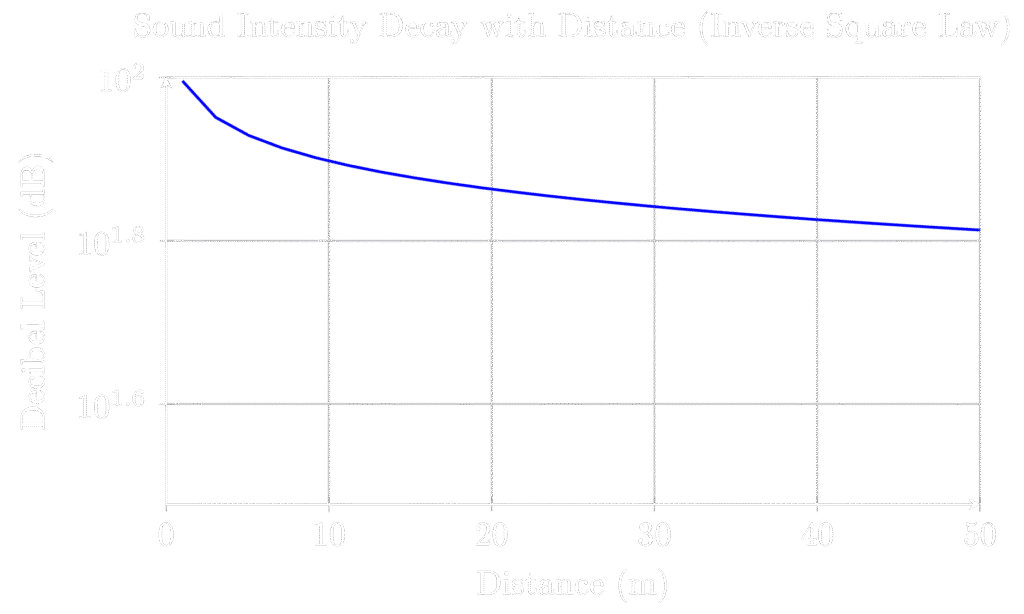
Just as sound waves propagate through a medium, their intensity also changes with distance. The figure below demonstrates how the decibel level of a sound source diminishes as you move further away, following the inverse square law.

Conclusion

Even with all the music, communication systems, diagnostic tools, and computational models that rely on it, sound still hides secrets. Scientists have been studying it for centuries, and they still don’t fully agree on every aspect of how complex soundscapes are perceived and processed by our brains.

Sound might just seem like noise or music, but it’s actually a very complicated concept that we can’t fully grasp today. The next time you hear that gentle hum or feel the bass vibrating through you, smile at the underlying physics. You’re witnessing countless particles vibrating in intricate patterns, a scene that reminds us of how physics is so deeply embedded in our natural world, forming its own hidden orchestra.