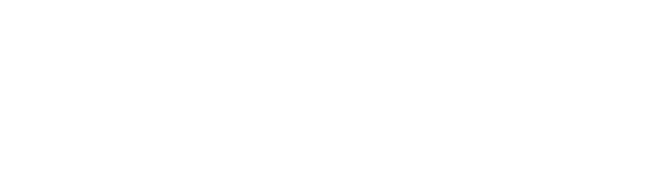It’s midnight. You’re standing in a quiet valley. The mountains around you fade into dark silhouettes, and the starlight above fills you with excitement for a night of stargazing through your telescope. You focus on what looks like a bright star with a tiny blemish. You adjust the focus, and in a breath of realization, you find that it’s not a star at all, but Jupiter, distant yet luminous. You wonder about the long journey of each photon, reflected from Jupiter’s cloud tops, crossing the cosmic sea to meet your gaze. The answer is something we have never known in classical Newton’s equations. It lies in Einstein’s general relativity. Jupiter large mass causes a curvature in a geometrical shape known as the Curvature of space-time, bending the path those photons follow, so that without you even noticing, Jupiter is subtly changing not just your view of the universe, but also the moment in time you’re experiencing.

Bending of Light – From the Sun to Black Holes

The idea of light deflecting near massive objects like Jupiter, the Sun, and black holes was just a bold prediction in Einstein’s general relativity that everyone was skeptical of. However, in 1919, when Sir Arthur Eddington led an expedition to observe a total solar eclipse, scientists photographed stars located behind the Sun, and to their surprise, the stars’ apparent positions had shifted slightly outward. The cause? Light from those stars had bent as it passed near the Sun’s mass. This was the first experimental proof that gravity can deflect light in phenomena called gravitational lensing.

The above figure shows the observed angle of light bending, to get this mathematically, the deflection angle for light passing at a distance R from a spherically symmetric mass M is given by:

\theta\approx\frac{4GM}{c^2b}

Substituting near the Sun’s limb:

\theta_\odot\approx\frac{4GM_\odot}{c^2b_\odot}

This turns out to be:

\theta=\frac{4\times\left(6.674\times{10}^{-11}\right)\times\left(1.989\times{10}^{30}\right)}{\left(3\times{10}^8\right)^2\times\left(6.96\times{10}^8\right)}

\\=8.066\times{10}^{-8}\ \mathrm{rad}=1.75\ arcsec

The Spacetime fabric and time dilation

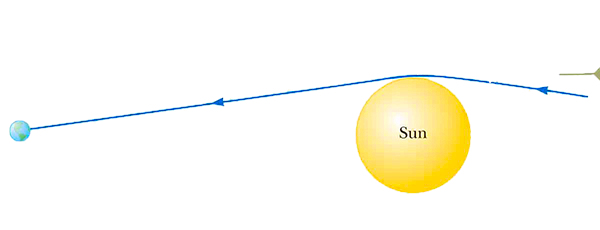
What we observed above was the fabric of spacetime, the plane in which light and every other particle moves in, and its deformation. This fabric not only bends the path of light around massive celestial bodies in the universe, but it also affects the flow of time (the fourth dimension in the fabric’s composition). Entertain this thought: Hold two clocks in your mind, clock 1 on the Mount Everest summit, and clock 2 at sea level. Weirdly enough, you’ll find that the clock located at sea level will be a little slower than the clock located at the top of the mountain. This happens due to gravitational time dilation, where time runs differently, in the same frame of reference, depending on how deep one is in the gravitational well. This effect becomes extreme near black holes; a few hours near the event horizon will be years to a distant observer.

Time difference between sea and Mount Everest:

\frac{\Delta\dot{\tau}}{\dot{\tau}}=\frac{GM}{c^2}\left(\frac{1}{r_{\mathrm{sea}}}-\frac{1}{r_{\mathrm{everest}}}\right)-\frac{v_{\mathrm{sea}}^2-v_{\mathrm{everest}}^2}{2c^2}

=9.6577\times{10}^{-13}\Rightarrow\Delta\tau_{\mathrm{per\ day}}\approx83.44\ \mathrm{ns/day}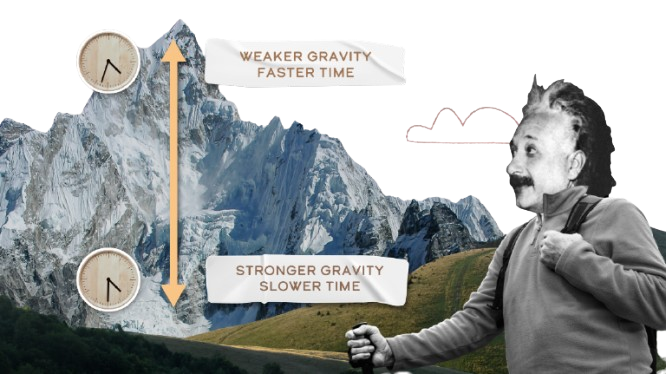

This effect is so significant that satellites running the GPS have to account for gravitational time dilation because, combined with the effect of their speed, their onboard clocks tick faster than those on Earth by about 38 microseconds per day. Without correcting this, your location on the phone’s map would be kilometers off within hours.

Gravitational time dilation effect on a GPS satellite:

\frac{\Delta\dot{\tau}}{\dot{\tau}}=\frac{GM}{c^2}\left(\frac{1}{r_{\mathrm{E}}}-\frac{1}{r_{\mathrm{S}}}\right)-\frac{v_{\mathrm{S}}^2-v_{\mathrm{E}}^2}{2c^2}

=\frac{3.986004418\times{10}^{14}}{\left(2.99792458\times{10}^8\right)^2} \times\left(\frac{1}{6378137}-\frac{1}{26578137}\right)-\frac{\left(3872.6355\right)^2-\left(465.1\right)^2}{2\left(2.99792458\times{10}^8\right)^2}

=5.2848\times{10}^{-10}-8.2230\times{10}^{-11}

=4.462\times{10}^{-10}\Rightarrow\Delta\tau_{\mathrm{per\ day}}\approx38.56\ \mu\mathrm{s/day}

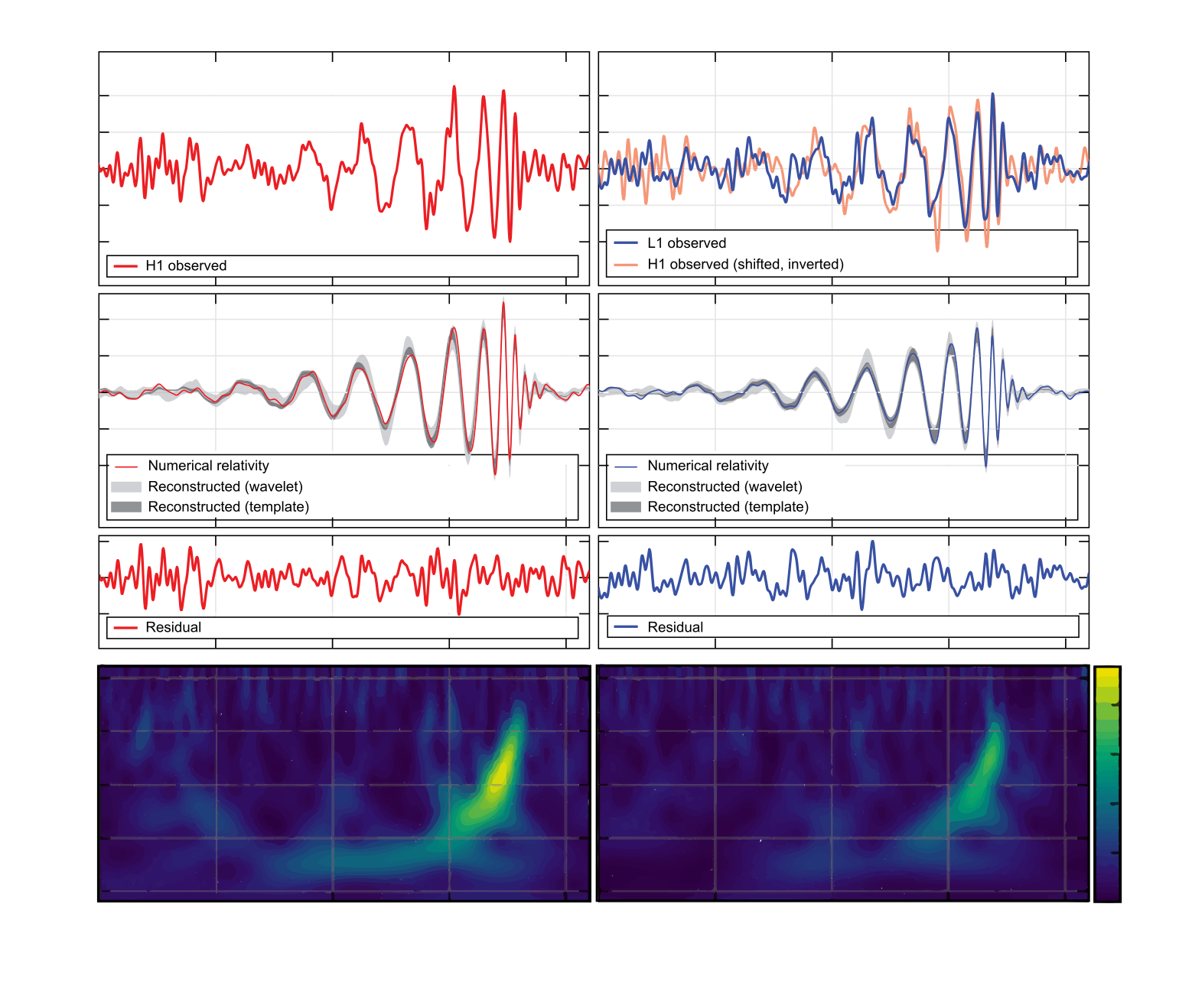
This very spacetime fabric of the universe could vibrate like a guitar string! Weird right? That’s exactly what happens in ringdown, the final stage after two black holes or 2 neutron stars merge, where they generate, or more accurately “generates”, since they merge and become one, subtle vibrations in spacetime. These vibrations are not sound, but rather gravitational waves that travel through the universe at the speed of light. The first detection of gravitational waves was made in 2015 by gravitational wave detectors, shown in the following figures.

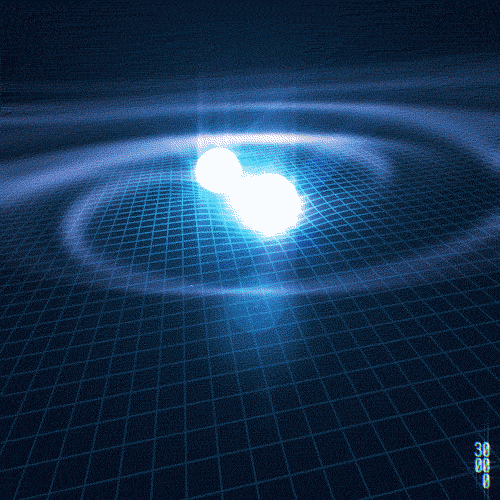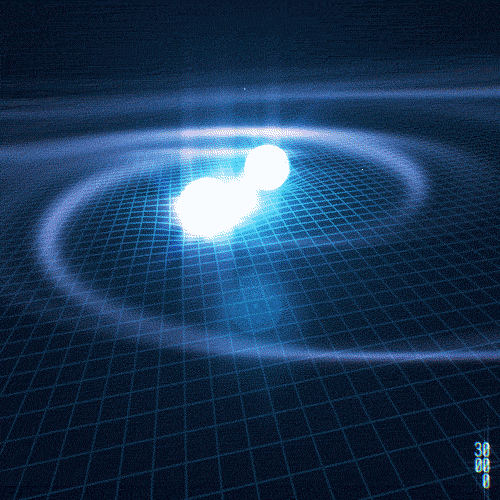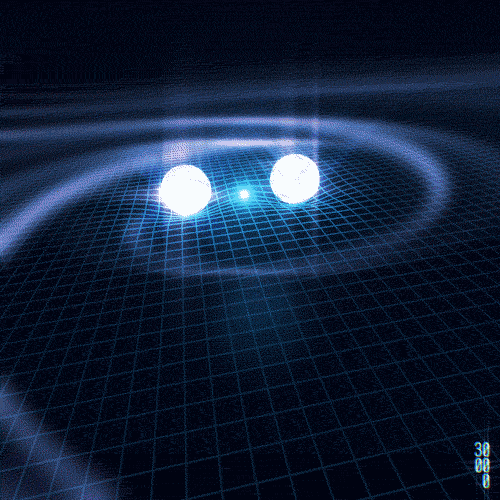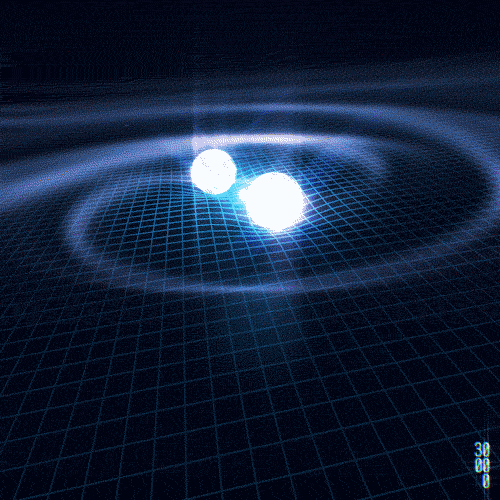
Wormholes

As Einstein’s equations determined the behavior of the space-time fabric around massive objects, they can also predict the existence of “wormholes.” Wormholes, also known as Einstein–Rosen bridges, are hypothetical tunnels in spacetime that could connect two distant points in the universe. The following solutions to Einstein’s equations of general relativity demonstrate that spacetime can be curved and linked in unusual ways. We can say that the wormhole would have 2 “mouths” and a “throat” connecting them. and entering through one mouth could instantly land you in the other. However, the conditions required to create or maintain a passage are extreme, and scientists have never observed any in the vast universe until now.

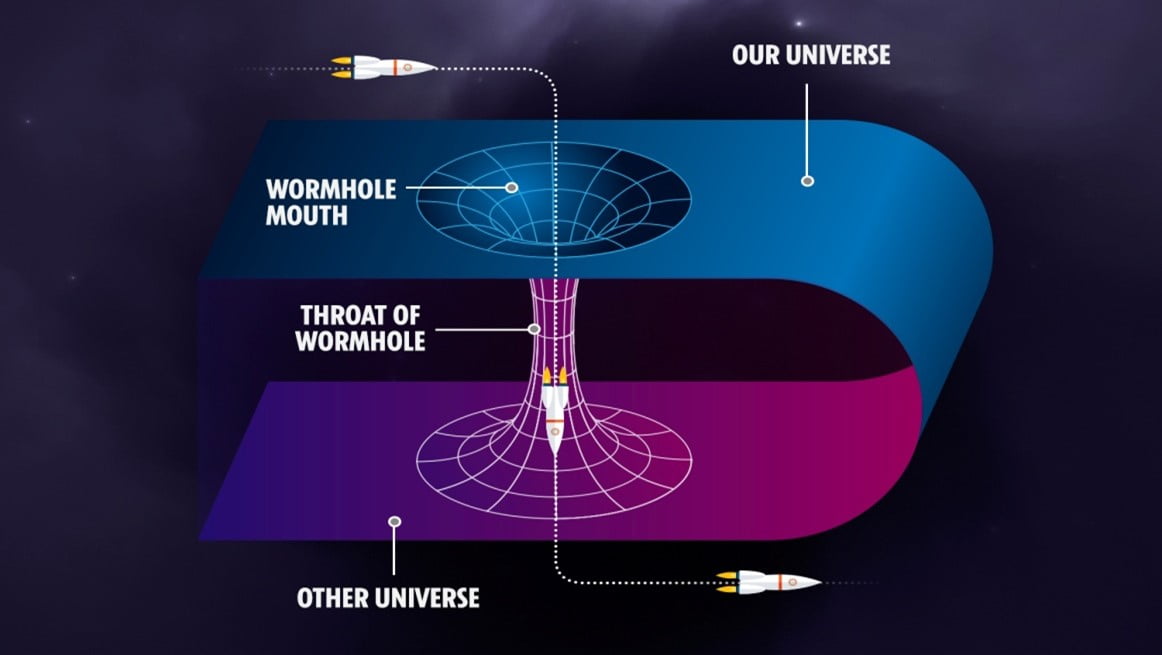
One of the major challenges with wormholes is stability. Without some form of “exotic matter” with negative energy density. A wormhole would collapse almost instantly. Even if such a matter exists and could keep the throat open, passing through might still expose travelers to immense gravitational forces and radiation. Furthermore, questions are being raised about causality. A traversable wormhole could theoretically allow for time travel, leading to paradoxes. While still a fascinating concept in both physics and science fiction, they remain more of a mathematical possibility than an experimental reality. Now, they represent the strange and flexible fabric of spacetime.

Conclusions

For over a century, general relativity has taken us on an extraordinary journey through the universe’s deepest secrets. We have seen light bend around the Sun, time slow down near massive objects, and the mystery of gravitational waves propagating through spacetime. Even science fiction ideas, like wormholes, have found a place within Einstein’s equations. However, they still belong to the realm of possibility. Every discovery was not the end of the story, but the beginning of a new chapter that opens up deeper questions.