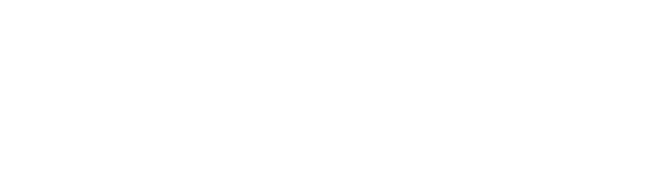The good ol’ double-slit experiment

Imagine tossing a marble at a wall with two open windows. You’d expect it to go through just one of them, as any normal particle would. However, unexpectedly you find that the marble goes through both windows at once and leaves behind an interference pattern, a bunch of streaks on the other side, which should be impossible as this is the behavior of a wave! This is the best analogy for the behavior of electrons and photons, explained by wave-particle duality. This concept was first proposed by Einstein in his third paper, “The photoelectric effect”, published in 1905. In an experiment, he found that, by focusing light with a certain frequency, independent of its intensity, an electron is ejected to a higher energy level, as proposed by Planck later.

E=nhf

This experiment shows that light has a particle behavior represented by photons, but in other experiments, light also showed interference patterns, which is a wave property, therefore, he assumed that light acts like both a particle and a wave. Later, Louis de Broglie proposed that matter also exhibits wave-particle duality, referring to electrons as exhibiting wave-particle duality as well. A mysterious experiment was done, which was nicknamed the heart of quantum mechanics. This experiment showed the mystery of microscopic physics and how Newtonian mechanics break down on the microscopic level. It is this experiment that gave birth to the science of quantum mechanics: the double slit experiment.

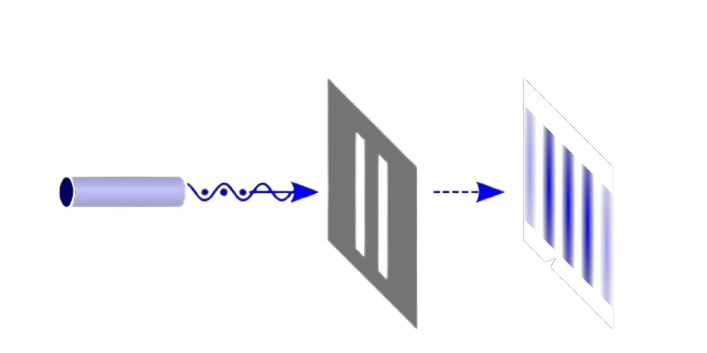
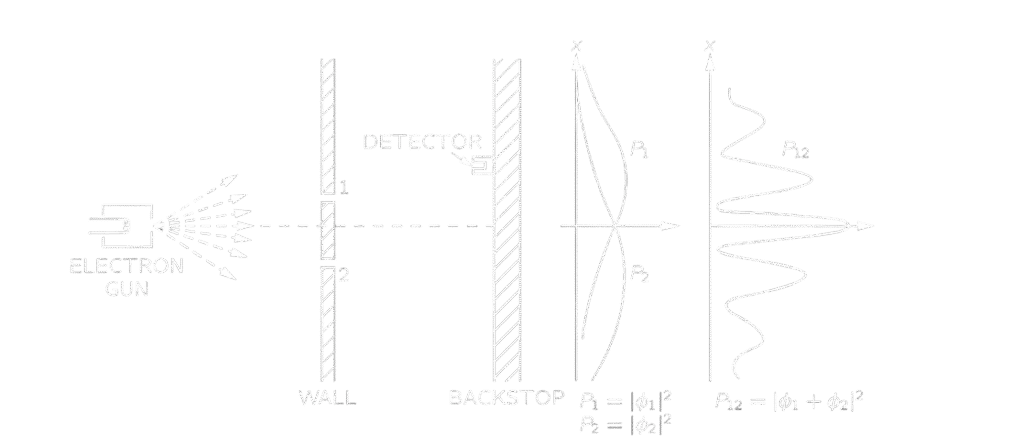
This experiment has been performed to test the behavior of electrons. An electron gun has been placed in front of a thin wall with two slits placed close with a detection screen behind. Moving through the experiment, electrons unexpectedly formed an interference pattern on the detection screen. Such a pattern looks like that of the wave behavior, but how shouldn’t electrons, which up we understood to be particles, be passing through either slit 1 or 2? For better clarification, let’s explain in terms of probability.

Probabilities, experiments, and math to explain what is going on!

Looking for analogy, we perform two experiments, one for particles,” bullets,” and the other for waves, “water waves.” For the bullet experiment, a bullet goes either through slit 1 or slit 2, so the probability of a bullet arriving at the detection screen is the sum of that passing through slit 1 and slit 2 simply.

P_{12}=P_1+P_2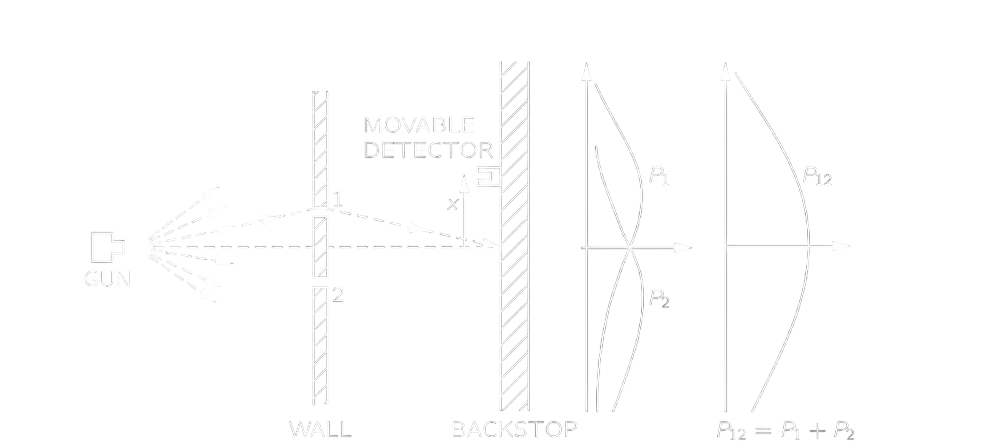 

Now, for the wave experiment, an interference pattern occurs, so it is definitely not the sum as that for bullets, but the squared sum of their amplitudes.

I_{12}=|h_1+h_2 |^2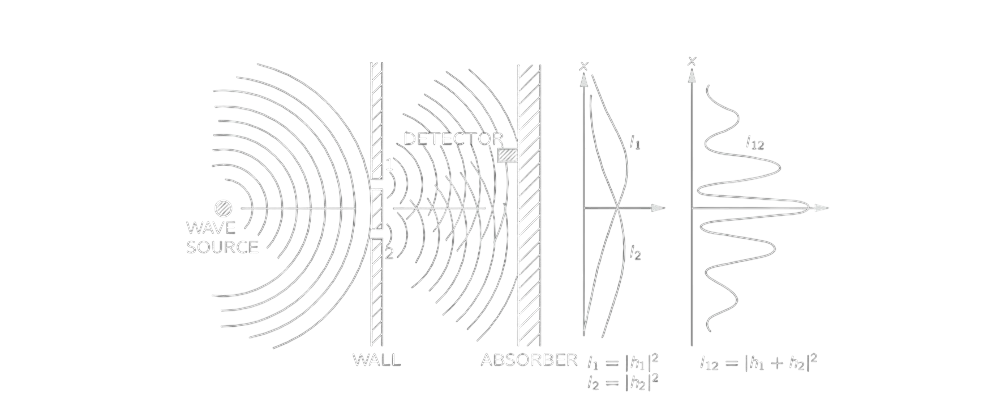

Looking back on our electron experiment, it looks exactly like that of the wave one. So finally, we conclude that electrons behave like waves! I am sorry to say it, but no! We do another experiment, as usual. During the experiment, a speaker has been attached to the detection screen that, for every electron arriving on it, the speaker makes a “click” sound. Every time an electron arrives, it is the same sound, not even a half “click”. So, it is obvious that electrons arrive in lumps, “complete electrons.”, meaning that, electrons indeed are a particle. But how? Is it both a wave and a particle?

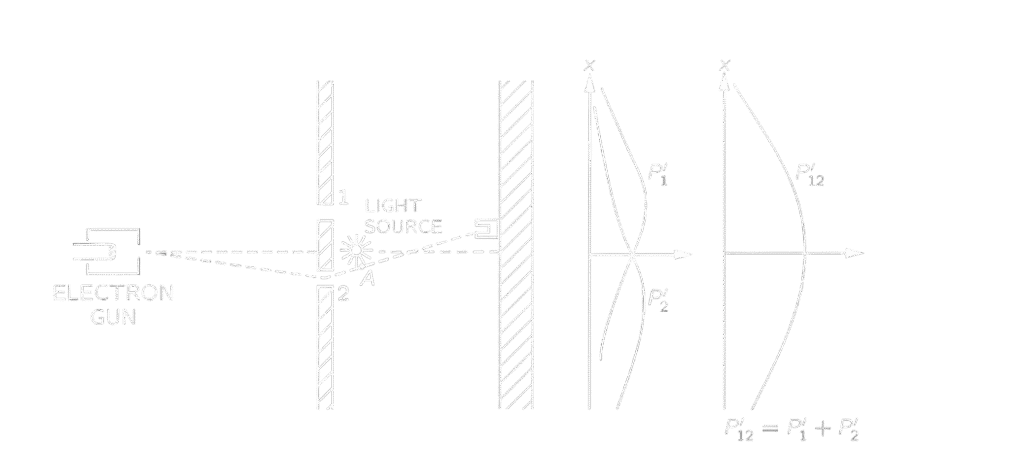
Let us make some assumptions to explain this behavior. First: electrons pass either through slit one or two. For such an assumption to happen, the probability will sum up, making a curve like that of the bullet experiment, but this is not the case. Two: electrons split in half and then interfere together. It is also not the case, as we said before, that electrons arrive in complete lumps. Maybe electrons move in a sneaky way? But how to experiment such an assumption? We can place a light source behind the slits that, for every electron passing a flash is produced letting us know where do the electrons pass. And here comes the surprise, the interference pattern is lost! Also, electrons seem to pass either through slit 1 or slit 2. But why?

Want to try and collapse Quantum Mechanics?

This happened because electrons interact with light photons, leading to a disturbance. But how could we now know the position of electrons? Long story short, we can’t. It seems that our electrons are in a state of quantum superposition, a way that we can’t explain in a classical way. Heisenberg proposed that nature has a law that puts a limitation on experimental capabilities, introducing it as the uncertainty principle, which stated in terms of our experiment: “It is impossible to design an apparatus to determine which hole the electron passes through, that will not at the same time disturb the electrons enough to destroy the interference pattern.” The complete theory of quantum mechanics depends on the correctness of Heisenberg’s uncertainty principle. However, if a way is discovered to beat the uncertainty principle, the quantum theory will be discarded as a valid theory of nature. In a more specific manner, the uncertainty principle states that if you can measure the position of a certain body accurately, you can’t at the same time know its momentum.

∆x∆P_x≥\frac{h}{4π}

In other words, as the uncertainty in the momentum approaches zero, the uncertainty in the position approaches infinity, meaning that you cannot find the electrons anywhere in the universe! At a first glance, it may seem like utter nonsense, you might say “Then, why can we calculate both the momentum and position at the same time in a classical sense? Does this mean that classical mechanics is wrong? Or is quantum mechanics wrong?” Actually, both are almost correct, but how? In 1924, De Broglie proposed that even particles have an associated wavelength.

λ=\frac{h}{p}

Using the above equation, we can find out that for large objects, the wavelength becomes extremely small (having very small ℏ) that the effect of the uncertainty principle can be neglected. Using this knowledge, we can have a different look at the particle experiment. It seems that even bullets have interference patterns!! It turns out that for bullets, the wavelengths were so tiny that the interference pattern became so fine. What we saw was a king of average, “the classical curve.” Additionally, there are many experiments that have been designed to prove the correctness of the uncertainty principle. It seems that the uncertainty principle protects quantum mechanics. Heisenberg recognized that if it were possible to calculate the momentum and the position together with great accuracy, quantum mechanics would collapse, so he proposed that it was impossible.

Alas, we reach the conclusion…

Many experiments have been designed and tested, and numerous scientists have tried, but no one has been able to do it, to disprove the uncertainty principle, to collapse quantum mechanics. Quantum mechanics maintains its perilous, but still verily correct existence. Quantum mechanics is the basis of Newtonian mechanics, they are not opposite in any way, rather they are fairly related, and we see their effects in nature equally.